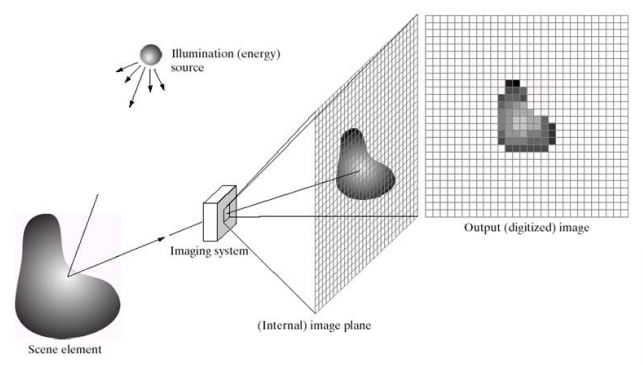
Image coding refers to the conversion of an image into a digital format for storage, transmission and reconstruction. In the context of image formation, the object that is being captured by a camera gets divided into a grid, which represents the process of dividing an image into pixels during image acquisition. These pixels contain information about the brightness and color of the image, which is then converted into a digital signal for storage or transmission.
By representing the two grids one next to the other, we can observe how the actual image has to be converted into a pixel-dominated representation that will lower the amount of details the image provides—based on the number of pixels that are used to store such image.

Therefore, during the process of acquiring the image, sampling and quantization are applied.
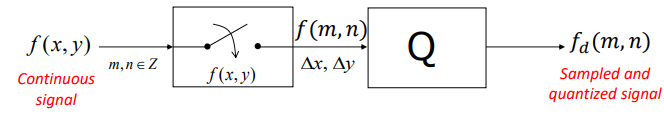
In a similar way to signal processing. In fact, for images, instead of applying sampling and quantization in the time domain, we apply it in the space domain, in which all pixels are delt with at the same time.
We can express the sampling function as
\color{white}f(m, \, n) := f(m\Delta x, \, n\Delta y)Where \Delta x and \Delta y are the sampling period along x and y respectively.
For the quantization we can instead write
f_d(m, \, n) = Q[f(m, \, n)]
In the context of image processing, we represent the sampled image through mathematical functions at discrete intervals. In the case of grayscale images, we consider the extremes as white and black, representing everything in the middle.
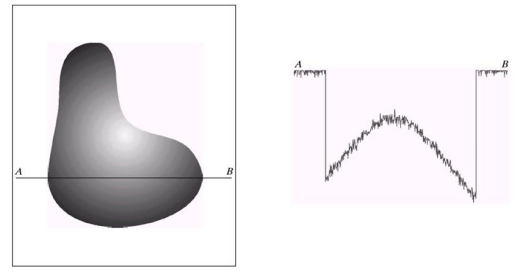
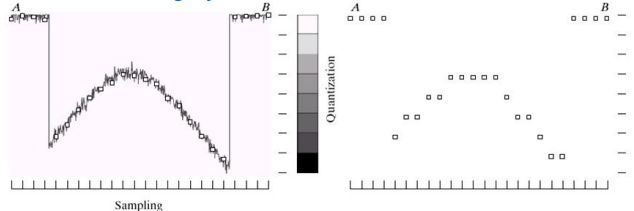
Which we can then turn into a quantized version depicted on the right.
Extending a line-representation sampling to a full image we get a 3D representation.
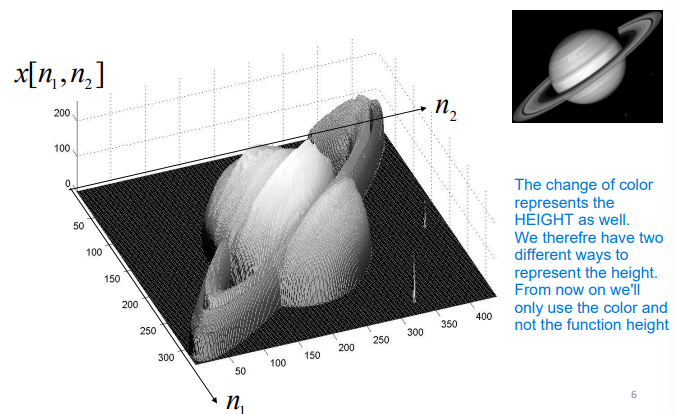
Which we can flatten by representing the third dimension by using just the color.
In the case of color images, we can deconstruct the RGB channels separately and represent a colored picture
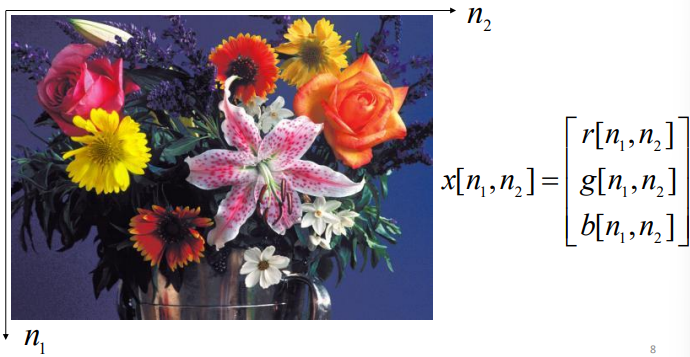
By leveraging the three different channels on their own into distinct representations.

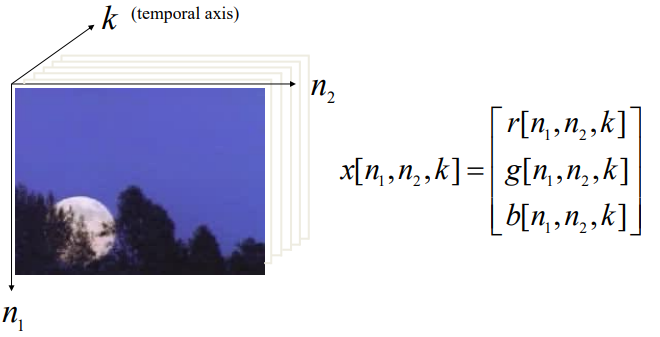
If instead of an image we want to code a video we also need to have the k time dimension together with the RGB representations.
Spatial resolution
We define spatial resolution as the smallest detectable detail in the image, that is the number of pixels per unit distance. For example, by reducing the number of pixels in an image, we get

And if we want to keep the image sizes constant, we can more clearly see how the smallest detectable detail changes by reducing the number of pixels

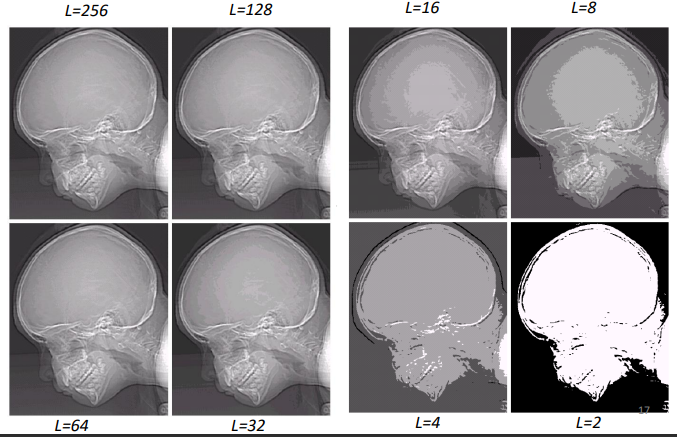
Gray level resolution and contrast
In the case on gray levels, the resolution is the smallest detectable change in gray level.
On the other hand, we can define contrast as the difference between the highest and lowest intensity level in the image.
For example, by reducing the number of gray levels we increase the contrast, as there are not as many shades of gray to be used to represent the transitions between the different parts of the image