Morphological operators operate on the shape and structure of objects within an image, enabling tasks such as noise reduction, edge detection, and object segmentation. By altering the geometric attributes of image regions, morphological operators play a pivotal role in enhancing image features, extracting relevant information, and preparing data for further analysis through operations like dilation, erosion, opening and closing.
The way they work is based on set theory and the images are usually binary (b/w). A set-based description of an image can be seen as a vector of tuples, each tuple representing the (x, \, y) coordinates of a point belonging to the set. We can process an image by adding or removing pixels to/from a set. We’ll look into the following methods:
- Erosion
- Dilation
- Opening and closing
Erosion
Erosion operates by shrinking or wearing away the boundaries of objects within an image, thereby effectively reducing their size and smoothing their contours. By systematically removing pixels from regions of interest based on predefined structuring elements, erosion can be used for noise elimination, edge detection, and object segmentation.
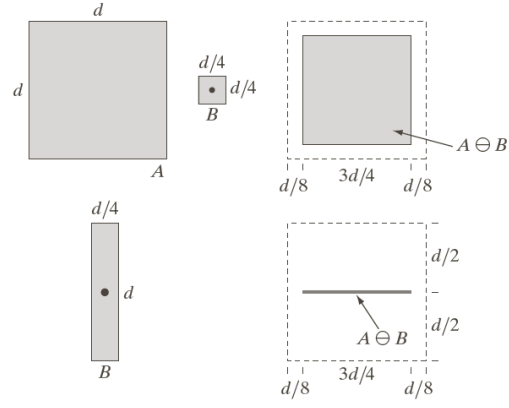
Let’s consider two sets, A and B (B is called the structuring element—see below for details). The erosion or A by B is defined as
A \ominus B = \{z \mid (B)_z \subseteq A\}In words: (B)_z signifies that the center of set B is in z. The center of B is continuously moved in z. The erosion operation keeps a point z if and only if the whole structuring element is fully included in A.
A structuring element is a small, pre-defined pattern or shape used to probe and modify the image. It serves as a kernel that defines the neighborhood around each pixel in the image. Structuring elements come in various shapes, such as squares, circles, rectangles, or more complex shapes, and sizes, which can be adjusted based on the specific requirements of the erosion operation.
During the erosion process, the structuring element is systematically moved or through the image, centered at each pixel. At each position, the structuring element is compared with the neighborhood of pixels in the image. If the structuring element completely overlaps with the object or feature of interest in the image, the corresponding pixel in the result is preserved; otherwise, it is removed. This process effectively erodes or shrinks the size of the objects in the image, smoothing their boundaries and eliminating smaller details.
Examples of structuring elements can be seen below
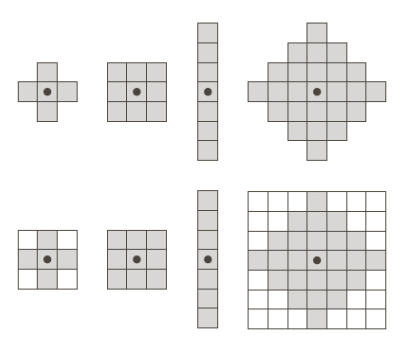
Where in the bottom row the structuring elements have been converted to rectangular arrays
For example, by applying erosion with the structuring B shown below to the shape A we get a version of A in which its size is shrunk.
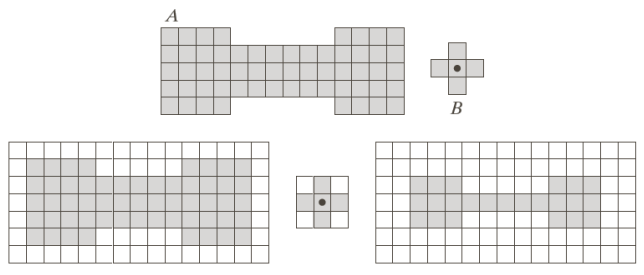
The shape of the structuring element determines in which direction the erosion operates. For example, in the image below, by using a square structuring element the image is just shrunk keeping the original proportions, while by using a more elongated one the final image looks very different
Through this process we can remove image components. By using structuring elements of increasing size, we can see that in each of the images below the final image contains less and less details.

Dilation
Dilation operates by expanding or enlarging the boundaries of objects within an image, thereby effectively increasing their size and emphasizing their presence. By systematically adding pixels to regions of interest based on predefined structuring elements, dilation can be used for feature extraction, texture analysis, and object segmentation.
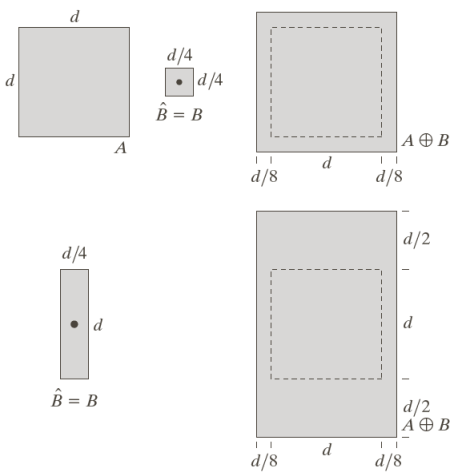
As we did with erosion, we consider two sets A and B, where B is the structuring element. Dilation is defined as
A \oplus B = \{ z \mid (B)_z \cap A \neq 0\}In words: the structuring element B is moved continuously in the pixel z and z is kept if and only if there is at least one pixel overlapping with A.
As seen before, varying the shape of B leads to different results in the final dilation. For example
A practical application of this is the enlarging of text characters to make them more readable.

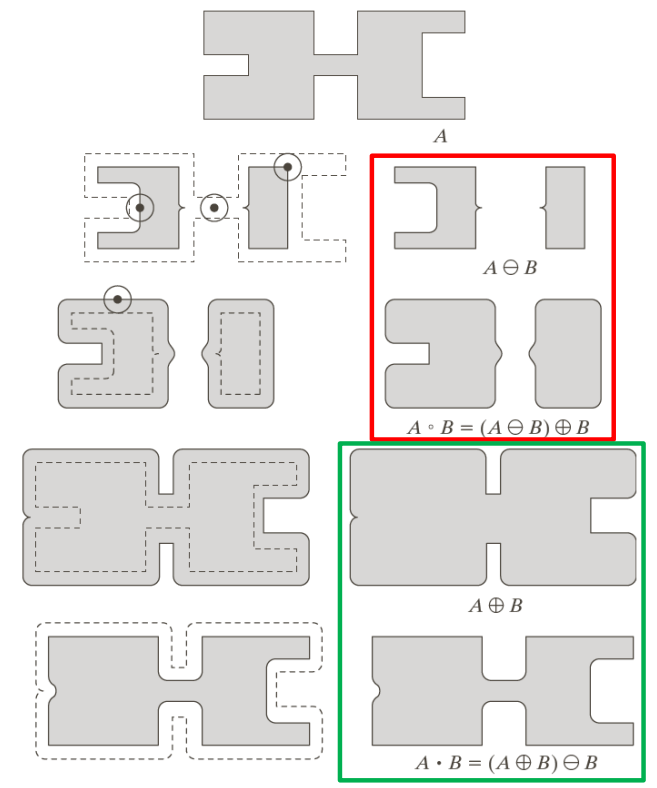
Opening and closing
Opening, consisting of an erosion followed by a dilation, acts as a noise-reduction mechanism by removing small-scale structures and smoothing object boundaries while preserving the overall shape of larger features. Conversely, closing, which involves a dilation followed by an erosion, serves to bridge small gaps between object contours and fill in narrow breaks, enhancing object connectivity and completeness within the image. By harnessing the complementary nature of opening and closing operations, computer vision systems can effectively enhance image quality, improve object delineation, and facilitate robust interpretation of visual data.
Mathematically, we can express such operation as
A \circ B = (A \ominus B) \oplus B
Which has the effect of smoothing the contours and eliminating protrusions without reducing the element size, or, similarly, we can also fuse narrow breaks without increasing the element size by inverting the order of the operations
A \circ B = (A \oplus B) \ominus B
Visually, these two effect result in
And by combining opening and closing multiple times, a lot of effects can be obtained