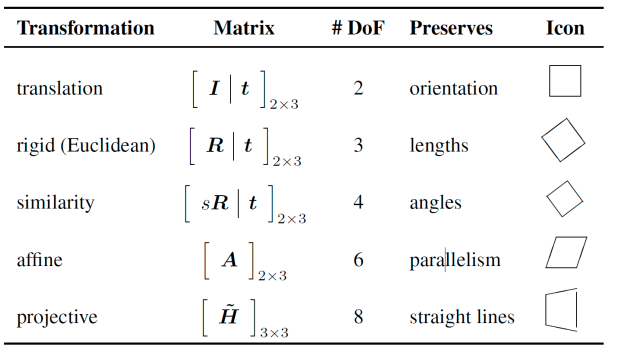
Geometric transformations are operations that modify the spatial arrangement of the pixels within an image. For example:
- Translation: Shifting the image along the x and/or y-axis.
- Rotation: Rotating the image by a specified angle.
- Scaling: Enlarging or reducing the size of the image.
- Shearing: Distorting the image by shifting one part of it in a particular direction.
- Reflection: Flipping the image horizontally or vertically.
- Affine Transformation: Combining translation, rotation, scaling, and shearing in a linear transformation.
- Perspective Transformation: Simulating a change in viewpoint, useful for correcting distortions caused by the perspective of a camera.
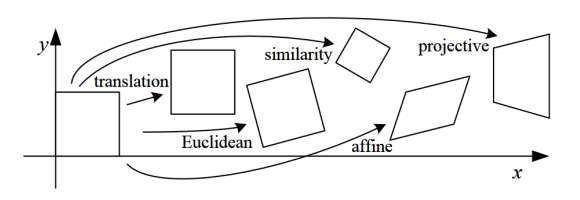
The coordinate transformations work on geometrical points that convert the image from one coordinate system to another. To do this we can use matrices, specifically
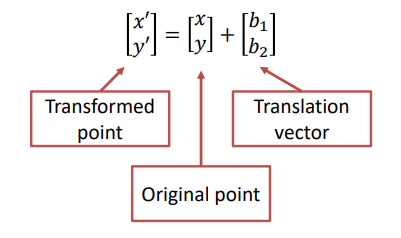
For example, in the case of a translation, we get
Homogeneous coordinates
To represent points in 2D space we can use homogeneous coordinate, which allow us to represent transformations in a more compact way by using matrix multiplication only.
We therefore get vectors that can convert the numbers from one coordinate system to the other, and vice versa.
- To homogeneous coordinates
\begin{bmatrix}
x\\
y
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
\widetilde{w} \, x\\
\widetilde{w} \, y\\
\widetilde{w}
\end{bmatrix}
=
\begin{bmatrix}
\widetilde{x}\\
\widetilde{y}\\
\widetilde{z}
\end{bmatrix}- From homogeneous coordinates
\begin{bmatrix}
\widetilde{x}\\
\widetilde{y}\\
\widetilde{w}\\
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
\widetilde{x} / \widetilde{w}\\
\widetilde{x} / \widetilde{w}
\end{bmatrix}In the case of translation we have
- Translation
\begin{bmatrix}
x'\\
y'
\end{bmatrix}
=
\begin{bmatrix}
x\\
y
\end{bmatrix}
+
\begin{bmatrix}
b_1\\
b_2
\end{bmatrix}- Translation from homogeneous coordinates
\begin{bmatrix}
x'\\
y'\\
1
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
1 & 0 & b_1\\
0 & 1 & b_2\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}- Yelding (shifting the point (x, \, y) by b_1 units horizontally and b_2 units vertically)
\begin{bmatrix}
x'\\
y'\\
1
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
1 & 0 & b_1\\
0 & 1 & b_2\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
=
\begin{bmatrix}
x+b_1\\
y+b_2\\
1
\end{bmatrix}Affine transformations
We will now take a closer look at the affine transformations. This kind of transform preserves the point co-linearity and the distance ratios along a line

We can express it by using a linear transformation followed by a translation, which we can then convert into homogeneous coordinates
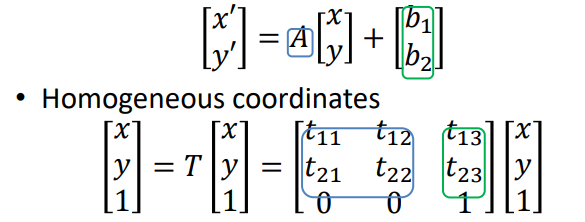
Other examples of affine transformations are reported below
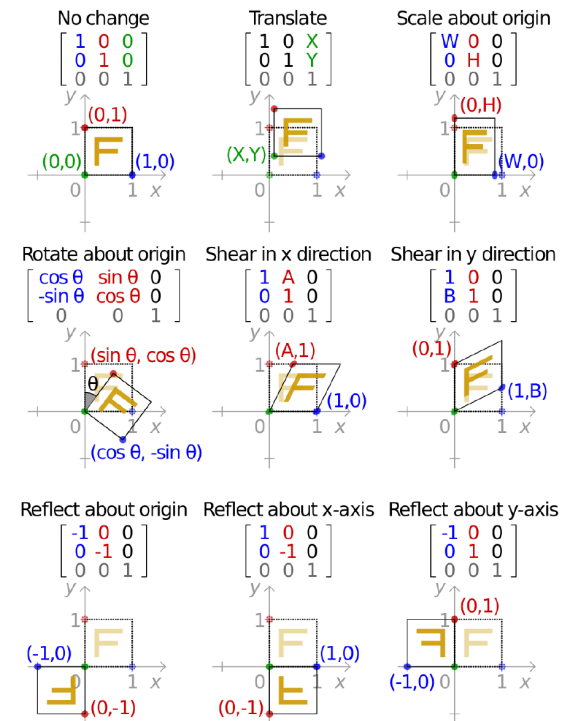
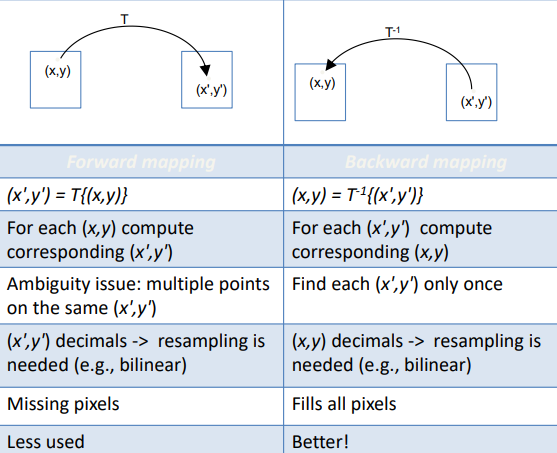
Forward vs backward mapping
In forward mapping, each pixel in the source (original) image is mapped to a position in the destination (transformed) image. However, forward mapping can sometimes leave gaps (unfilled pixels) in the destination image, especially with complex transformations.
In backward mapping, each pixel in the destination image is traced back to a corresponding position in the source image. This approach is often used to ensure that every pixel in the transformed image has a value, avoiding gaps but requiring interpolation to fill in missing values if the exact source pixel doesn’t exist.
Affine transformations in OpenCV
void cv::warpAffine(
CV::InputArray src, // input image
cv::OutputArray dst, // output image
CV::InputArray M, // 2x3 transform matrix
CV::Size dsize, // destination image size
int flags = cv::INTER_LINEAR, // interpolation, inverse
int borderMode = cv::BORDER_CONSTANT, // handling of missing pixels
const cv::Scalar& borderValue = cv::Scalar() // constant borders
);The OpenCV docs related to this topics can be found here.