Introduction

In machine learning, our aim is to create a system that can improve itself at a task T according to some performance metric P, by trying to find a function that best fits the training data \mathcal{D} — where we want to minimize the difference with respect to the original one.

The training can be:

• Direct: provides feedback on each move.
• Indirect: provides feedback only when the final outcome is known.

Distinguishing between what nodes of the network made the best choices is thus known as the credit assignment problem.

There are three main kinds of learning:

• Supervised learning
• Unsupervised learning
• Reinforcement learning

We want to find an operational description \widehat{V}of the ideal target function, which fits the ideal target function as closely as possible. We want \widehat{V} to be highly expressive, and at the same time as simple as possible. We run into a tradeoff: the higher the expressivity of the function, the more resources it needs, and thus finding a good balance between these is crucial.

Target functions are not unique, so similar functions create a model class, also known as a hypothesis space.

Types of ML

• Supervised learning: we have training inputs as a d-dimensional vector, and the corresponding responses (e.g., categorical values for classification or real-valued for regression).
  • Semi-supervised: the training set is divided into a labeled part and an unlabeled part.
  • Few-shot: we only give a few examples for the training process. It could also be 1-shot or 0-shot learning.
• Unsupervised learning: finds patterns in the data autonomously without pre-labeled data. This might, for example, entail a projection into a lower dimensional space, or some clustering techniques being applied.
• Reinforcement learning

In many cases, models return a probability distribution of the various possible answers, with probabilities associated with them.

❓

• List and describe the three main types of machine learning.

Parametric vs. non-parametric models

A non-parametric model does not depend on a fixed number of datapoints, and thus always keeps the entire dataset available (eg. KNN). This can be really effective, but it might lead to computational inefficiencies as the number of dimensions increases.

💡

What’s a neighbor in a high-dimensional space?

The concept of neighborhood changes in high-dimensional spaces: in higher dimensions, neighbors tend to be farther apart, meaning there’s less meaningful neighborhood information.

A parametric model, on the other hand, estimates the values for a fixed set of parameters (coefficients), and the assumption that the problem can be effectively represented using such parameters is called inductive bias (eg. regression problems). This could sometimes lead to overfitting the data if we don’t choose number of parameters carefully (eg. in a polynomial regression problem, if we increase the number of parameters too much it might lead to overfitting).

Parametric models are usually faster and easier to use because of fixed storage and computational costs, but they rely on strong assumptions that might not hold, potentially hindering performance.

❓

• Contrast parametric and non-parametric models and give examples.

Model selection

When selecting a suitable model to solve a problem, we could try to just minimize the misclassification rate on the training data, but this is not not very effective because we are just testing the model using the same data we used for training. A better approach is to use a loss function which can calculate the misclassification rate of a model based upon what is known as generalization error, which describes the expected misclassification rate over future data.

To achieve such result, the original dataset we start with is divided into three sub portions:

• Training set (e.g., 70%)
• Validation set (e.g., 20%)
• Test set (e.g., 10%)

And we can now describe the difference between the training error and the expected error on future data as generalization gap.

Additionally, if we don’t have enough data, we can use K-fold cross-validation, which iteratively uses the three aforementioned sets in a way that ensures that every data point has an equal impact on all processes.

❓

• Why do we distinguish training, validation, and test sets? What would happen if training set = validation set? And if validation set = test set?

Training, inference, and Decision

When constructing a model, the first step is the training: the goal is to develop a suitable classifier by following one of the three main approaches:

1. generative models
2. discriminative models
3. discriminative functions

Once the model is trained, we can use it for inference, meaning we can predict an output for a new point. Often, this is achieved by determining the posterior class probabilities, which represent the probability of each class, given the training data.

Finally, the decision is made by assigning a class label to the class with the highest probability. A model might also refrain from making a final decision, if the inference step doesn’t yield high-enough probabilities.

❓

• What is meant by training, by inference, and decision? What are the respective inputs/outputs?

Discriminative functions

Discriminative functions directly map data to a class without using probabilities, thus they combine inference and decision and do not output the model’s confidence. This is an easy technique to use but predictions are risky since they don’t have any probabilities associated with them.

Examples: KNN.

Discriminative models

Discriminative models work on estimating the probability of a class label given a particular input, without modeling the underlying distribution of the input data itself.

Examples: logistic regression, KNN with probabilities.

Generative models

Generative models assume that both inputs and outputs can be modeled jointly.

They define how likely each class is overall (prior probabilities) and how the input data is distributed for each class (class-conditional densities).

If these assumptions hold, generative models may need less training data and be more accurate.

Examples: Naive Bayes, Generative Adversarial Networks (GANs).

❓

• Contrast discriminative functions, discriminative models, and generative models.

💡 Large Language Models (LLMs) also fall into the generative model category because they model the joint probability distribution of sequences of words. Specifically: p(\text{word}_1, \text{word}_2, \dots,\text{word}_n).
Using this, they can generate new sequences (e.g., text or answers).

Selecting the model parameters

Suppose we are given a parametric model class with parameters \boldsymbol \theta and some training data \mathcal{D}. Estimating the model parameters means estimating the values of \boldsymbol \theta using \mathcal{D}—which corresponds to the training phase.

We can use one of two techniques:

• Point estimates: we estimate all the values \hat{\boldsymbol{\theta}} from \boldsymbol \theta.

  Point estimation is a statistical method used to provide a single best estimate of an unknown parameter (e.g., the mean, variance, or probability of an event) based on observed data. The goal is to summarize the entire information about the parameter into a single value, called the point estimate.

• Posterior distributions: we just want to make predictions, thus we use p(\boldsymbol\theta\mid\mathcal{D}).

💡

Frequentist vs Bayesian interpretation of probability

• Frequentists: parameters have fixed but unknown values.
• Bayesian: parameters as random variables and associates them with probability distributions

❓

• What is the key assumption of frequentist methods? And of Bayesian methods?

Let’s consider a frequentist interpretation of probabilities where \boldsymbol\theta^* is the true parameter value. We can define the following concepts:

• Bias: expected difference between the estimated and true parameter values, averaged over repeated sampling from the data distribution.
• Variance: how much the estimator varies around its mean.
• MSE: average squared difference between the estimator and the true parameter.

Moreover, we have the bias-variance decomposition, which states that

Moreover, there exists the bias-variance tradeoff, which describes how with more data the variance in the model fit usually decreases, however, bias might not, as it depends on the model itself.

❓

• What is the bias, variance, and mean squared error of an estimator? What is the bias-variance tradeoff? Can you give a concrete example?

📢 We will continue to assume a frequentist interpretation of probabilities until we change to the Bayesian interpretation with a callout similar to this one!

Likelihood

The likelihood is defined as:

• For a generative model: probability of observing a specific dataset \mathcal{D} given the true parameter \boldsymbol\theta.
• A discriminative model: probability of the labels {\bf y} given the inputs \bf X and the parameters \boldsymbol\theta.

Intuitively, the larger the likelihood, the more consistent the data is with the parameter choice.

Maximum Likelihood Estimation (MLE)

📌 If I were a 5 year old…
Imagine you have a big bag of colored candy. You don’t know how many of each color are inside. You want to guess how many red ones there are, based on what you’ve seen so far.
Here’s what you do: you pick some candies from the bag and count how many are red. Then, you make a guess about how many red candies are in the whole bag.
If you pulled 10 candies from the bag, and 7 of them were red, you’d assume that about 70% of them are red. If that was true, we could in fact say that If 70% are red, it makes sense that I pulled 7 out of 10.
That’s what MLE does: it finds the best guess based on the data it has seen.\

MLE selects the values of \hat{\boldsymbol{\theta}} that best explain the observed data based on the likelihood function (conditional likelihood).

This is a very effective technique as large sample sizes make MLE asymptotically optimal in terms of mean squared error, however, it can be biased and prone to overfitting with small datasets.

❓

• Describe the framework of maximum likelihood estimation (MLE). Which desirable properties does MLE have? Which undesirable ones? Is the ML estimate unique?
• For MLE, why do we optimize the log-likelihood instead of the likelihood directly?

Empirical Risk Minimization (ERM)

ERM is based on the concept of risk, which refers to how well a machine learning model is performing, measured as the difference between the model’s predictions and the actual outcomes. We obviously want to minimize it. The true risk is the “ideal” measure of how good a model is using the actual (usually unknown) distribution, so in practice cannot be used. We thus use the empirical risk, which calculates the average error of the model on the training dataset.

When we minimize empirical risk we also hope it will reduce the true risk.

❓

• Why can’t we minimize the risk directly?

Minimizing the risk on the training data can lead to overfitting, as it approximates the training data too well. In order to mitigate the issue, we can include regularization. It combines empirical risk with a penalty term \lambda to create regularized risk.

❓

• In practice, we often use regularized risk minimization (RRM). Why?

This way, we can penalize model complexity to induce simpler models, ensuring the model fits the training data while also generalizing well to new, unseen data. Ideally, the penalty should align with the generalization gap.

💡

Learning theory and the size of the dataset\

we call version space the set of hypotheses consistent with the training data. Learning theory suggests that with sufficient training data, the version space is likely to contain fewer poor hypotheses. As the number of training samples increases, the likelihood of bad hypotheses being eliminated increases. In real life, we can rarely have all datapoints germane to the problem, thus the version space might contain bad hypotheses as well. To mitigate this, we can use PAC learning, which involves bounding the number of samples and computational cost needed to find a good hypothesis or VC dimension, which measures hypothesis space complexity, even when infinite.

❓

• Describe the framework of empirical risk minimization (ERM). Contrast with MLE.
• Discuss the use of a spherical Gaussian as a prior for a model’s parameters.
  – Assumes that the parameters follow a multivariate normal distribution with a mean vector of zeros and a covariance matrix proportional to the identity matrix.
• Discuss the use of L2 regularization for regularized risk minimization.
  – also known as ridge regularization, adds a penalty term proportional to the squared L2-norm of the parameters to the loss function. It is equivalent to weight decay.
• Relate these two approaches to each other. What is similar, what is different?
  – L2 regularization can be interpreted as using a spherical Gaussian prior in a Bayesian framework. Both approaches result in the same penalization term.
• What is meant by weight decay? How can we interpret it?
  – It is a regularization technique used in machine learning to prevent overfitting by adding a penalty to the size (magnitude) of the model’s weights during training. This way it does not become overly dependent on a specific feature.

Prior and Posterior Probabilities

📢
We will now assume a Bayesian interpretation of the probabilities!

We now switch to Bayesian models, which involves reasoning about beliefs, quantified as probability distributions.

We want to express how likely a parameter value is, based on prior belief, which incorporates prior knowledge about a parameter’s potential values.

The posterior belief then updates the prior belief using data, altering the initial assumptions that were made.

We have the following relationship:

Maximum A Posteriori (MAP) Estimation

The MAP estimate is the point estimate that maximizes the posterior probability, thus it represents the most likely parameter based on the posterior probability distribution. Finding the parameter estimate that maximizes the posterior distribution corresponds to maximizing the product of the likelihood and the prior distribution.

✏️

The Math

The fully Bayesian approach does not rely on estimating a single set of parameters. Instead, it evaluates all possible parameter values and combines their predictions, weighted by their posterior probabilities. By integrating over the entire parameter space, this method marginalizes the parameters, using their posterior distributions to make predictions for new data points. This ensures that predictions account for the full uncertainty in the parameter estimates. If I were a 5 year old… Imagine you’re trying to guess how many candies are in a jar, but you’re not sure of the exact number. Instead of picking just one guess, you think about all the possible numbers it could be—maybe 10, 20, or even 50. Now, you look at clues, like how big the jar is and how much space the candies take up. Based on these clues, you decide which numbers are more likely (for example, maybe 20 candies seem more likely than 50). When you make your final guess, you don’t just pick one number. Instead, you use a mix of all the possible numbers, with more “weight” given to the numbers that seem more likely. This way, your guess is smarter because it considers all the possibilities, not just one.

MAP vs MLE

MAP estimation can be seen as an extension of MLE. While MLE relies solely on the likelihood of the data, MAP incorporates prior knowledge or assumptions through a prior distribution. This additional information helps to reduce overfitting by favoring simpler or more plausible models.

❓

• Contrast MLE/ERM/RRM with Bayesian inference.
• Explain why the variance of the posterior predictive distribution of Bayesian linear regression may differ for different inputs. Contrast this with linear regression.
• In Bayesian inference, what is the role of the prior, the posterior and the>posterior predictive distribution? What does each distribution model?
• Describe the framework of Bayesian decision theory.
• In principle, can we compute the expected loss? And the Bayes estimator?
• Name and define the key distributions relevant to Bayesian inference. What is meant by fully Bayesian inference?

Generative Models for Discrete Data

📌 If a was a 5 year old… Imagine you’re playing a game where you have a big toy box filled with LEGO animals and trees. Every time you pull out a toy, you also see what kind of box it came from. We now aim to guess what’s inside a box just by looking at the toys.

1. First, we learn the patterns: You notice, “If there’s a monkey or a palm tree, it’s probably from the jungle box. If there’s a deer or a pine tree, it’s from the forest box.”
2. Then, when new toys show up we guess the box by thinking, “This looks like the jungle toys I’ve seen before!” A generative model thus learns how things go together (toys and boxes) by studying patterns. Then, when it sees something new, it makes a smart guess by using what it learned. On the other hand, a discriminative model wouldn’t need to learn those general patterns, but could just focus on the features that discriminate between classes.

Generative Models for Discrete Data focus on learning the underlying structure and distribution of data that consists of discrete values, such as text, categorical variables, or sequences. These models aim to generate new data points that resemble the original dataset by capturing patterns, relationships, and probabilities inherent in the data.

❓
How can we perform prediction with a generative model?

Performing prediction with a generative model involves leveraging its ability to model the joint probability distribution of inputs X and outputs Y and p(X, , Y) rather than just the conditional probability p(Y \mid X) as in discriminative models. We are thus trying to predict how everything is connected with each other, not just a single prediction on a sample.

We’ll look into the following models:

• The Beta-Binomial Model
• The Dirichlet-Multinomial Model

💡

Some distributions in a nutshell

The Beta distribution The Beta distribution models uncertainty in probabilities. It is defined on the interval [0, 1] and is controlled by two shape parameters, \alpha and \beta, which determine its shape.

• A larger \alpha makes the distribution skewed toward 1 (favoring higher probabilities).
• A larger \beta skews it toward 0 (favoring lower probabilities).

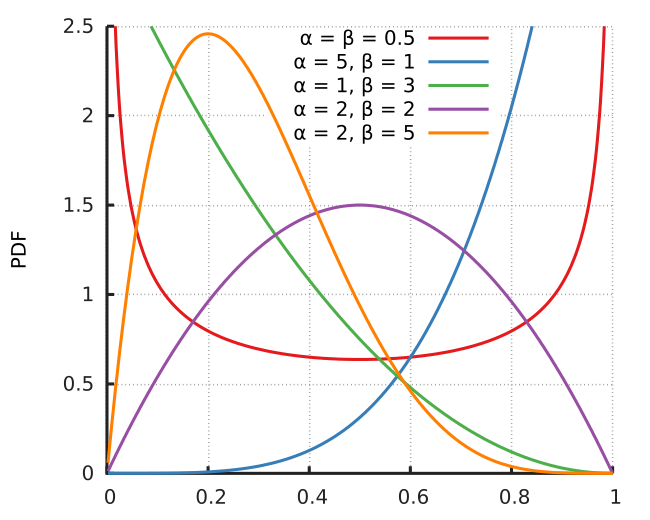
The Beta distribution is often used as a prior for probabilities because it can represent a wide range of beliefs (e.g., uniform, peaked, or skewed).

Dirichlet distribution

The Dirichlet distribution models uncertainty over a set of probabilities for K categories. It is a generalization of the Beta distribution to more than two categories and is defined over the probability simplex—the space where the probabilities for all categories sum to 1. It is the conjugate prior of the multinomial distribution (see below).

A symmetric Dirichlet distribution uses a single concentration parameter vector \vec{\alpha} for all categories.

When the concentration parameter is small katex[/katex], the probability mass is concentrated around single categories, leading to less uniform distributions. Conversely, a large alpha katex[/katex] results in more evenly spread probabilities, mimicking a uniform distribution, which is exactly obtained when \alpha=1.

The Bernoulli distribution

The Bernoulli distribution is a probability distribution for a random variable with two possible outcomes: success and failure. It is defined by a single parameter p, which represents the probability of success.

The Categorical distribution

The categorical distribution describes the likelihood of an event occurring out of a fixed number of categories. Each category has a probability associated with it, and the probabilities across all categories sum to 1.

The categorical distribution is often used to model discrete outcomes, and is the generalization of the Bernoulli distribution to more than two outcomes.

Multinomial Distribution

The multinomial distribution is a generalization of the Binomial distribution to more than two outcomes.

❓

• Describe the Bernoulli, binomial, categorical, and multinomial distributions. How are they related?
• Which “shapes” can the Beta distribution represent and with which hyperparameters? And the Dirichlet distribution?

The Beta-Binomial Model

The Beta-Binomial Model is a probabilistic framework that combines the Beta distribution and the Binomial distribution to model uncertainty in probabilities. It is particularly useful for scenarios where the probability of success in a binomial process is not fixed but instead follows a Beta distribution.

📌 If I were a 5 year old…
Imagine you’re tossing a coin, but it’s a special coin that doesn’t always have the same chance of landing on heads. Sometimes it’s more likely to land on heads, and other times it’s more likely to land on tails—but you don’t know for sure.
Instead of saying, “This coin always has a 50% chance of heads,” you say, “The chance of heads could be anywhere between 0% and 100%, but I think it’s more likely to be around 60%.”
The Beta distribution is like a way to describe all the possible chances for heads and how confident you are about each one. It helps you guess what the coin might do, even if the chance of heads changes every time you toss it.

By updating the Beta distribution with observed data, the model provides a flexible and interpretable way to represent uncertainty and make predictions.

The posterior distribution is calculated by multiplying the likelihood with the prior distribution (the Beta distribution for this model) and normalizing by the probability of the data.

📌 If I were a 5 year old…
Imagine you’re trying to figure out how likely a coin is to land on heads. You start with a guess about the coin (your prior), like, “Maybe it’s a fair coin, so heads and tails are equally likely.” That’s your starting belief.
Next, you toss the coin a bunch of times and see how many heads and tails you get. The change of seeing the head or tails (the data) is called the likelihood.
To update your guess after seeing the data, you mix your prior belief with what the data tells you (the likelihood). Finally, you make sure everything adds up correctly (normalizing).
The result is the posterior distribution, which is your new, updated guess about the coin based on what you saw!

❓
Describe the Beta-binomial model. What are its parameters and its hyperparameters? What do they present? How is prediction performed if we use a MAP estimate for the parameters? And if we use fully Bayesian inference?

Conjugate priors

Beta distributions are commonly used as conjugate priors in Bayesian statistics. A conjugate prior is a prior distribution that, when combined with the likelihood, produces a posterior distribution in the same family as the prior. This property simplifies calculations, making the analysis more efficient and straightforward.

❓
What are conjugate priors? Describe advantages and disadvantages of using a conjugate prior.

Posterior predictive distribution

The posterior predictive distribution can be used to predict the outcome of future coin flips using the Beta Binomial model.

✏️

The math

We are predicting the outcome of the next coin flip x_{n+1}, given the results of previous flips n_H—the number of heads observed so far. Since we don’t know the true probability of heads \theta, we use a Bayesian approach to update our beliefs about \theta using the prior and observed data, and then predict the next outcome.

The Formula

The posterior predictive probability p(x_{n+1} \mid n_H) is calculated as:

• In this equation, we know that

  (\spades)=p(x_{n+1}=1 \mid \theta)=\theta

  p(x_{n+1} \mid \theta) is the likelihood for the new coin flip given a specific value of \theta. For a coin flip, this is just \theta if x_{n+1} = 1, since \theta is the probability of heads. Note: We do not know the true value of \theta, though.

• p(\theta \mid n_H): This is the posterior distribution of \theta, which represents our updated belief about \theta itself after observing n_H heads (and thus n_T tails). In Bayesian terms, this posterior follows a Beta distribution with parameters \alpha and \beta:

  (\clubs)=p(\theta \mid n_H) = \text{Beta}(\theta \mid n_H + \alpha, n_T + \beta)

Why Integrate Over \theta,?

We don’t know the exact value of \theta (the true probability of heads). Instead, we consider all possible values of \theta and weigh them according to how likely they are, using the posterior p(\theta \mid n_H). This is called marginalizing out \theta, and it accounts for uncertainty in its estimation.

Conditional Independence Assumption

A key simplification is that the next coin flip x_{n+1} is conditionally independent of past flips n_H given \theta. In other words:

This means that once we know \theta, the past outcomes don’t provide additional information about the next flip.

Calculating the Posterior Predictive Probability

After applying the product rule and marginalizing out \theta, we arrive at:

Where:

• n_H is the number of heads observed so far.
• \alpha and \beta are the parameters of the Beta prior, representing our initial beliefs about \theta.

What Does This Mean?

The formula tells us the probability of the next coin flip being heads, based on:

1. The number of heads observed so far n_H.
2. Our prior beliefs about \theta (encoded in \alpha and \beta).
3. The total number of flips so far n = n_H + n_T.

This result shows that the posterior predictive distribution for the next coin flip follows a Bernoulli distribution with success probability:

Final remarks

• If we’ve observed many coin flips (n is large), the posterior predictive is heavily influenced by the data n_H.
• If we’ve observed few flips, the prior \alpha and \beta have more influence, reflecting our initial uncertainty about \theta.

The Dirichlet-Multinomial Model

Adding more possible outcomes to the coin-flip model (i.e., we don’t have a binary problem anymore), we can use a multinomial model that can take that into account using the categorical distribution.

✏️ The math

Instead of just heads or tails, imagine outcomes like rolling a die with K sides.

1. Categorical Distribution:

   We represent the probabilities of each possible outcome (1, 2, \dots, K) using a vector:

   \vec{\theta} = \begin{bmatrix} \theta_1 \newline \theta_2 \newline \vdots \newline \theta_K \end{bmatrix}

   Note: all the probabilities must add up to 1.

2. Observing Data:

   If we observe n_k instances of outcome k, we can summarize all observations in a vector:

   \vec{n} = \begin{matrix} n_1 \newline n_2 \newline \vdots \newline n_K \end{matrix}

   where n_1 + n_2 + \dots + n_K = n is the total number of observations.

3. Multinomial Distribution:

   Given the probabilities \vec{\theta}, the data \vec{n} follows a multinomial distribution:

   p(\mathcal{D} \mid \vec{\theta}) = \text{Mu}(\vec{n} \mid n, \vec{\theta}) = \binom{n}{n_1 \cdots n_K} \prod_{k=1}^K \theta_k^{n_k}

   The multinomial coefficient counts the number of ways to arrange the observations.

   The product \displaystyle\prod_{k=1}^K \theta_k^{n_k} gives the probability of observing the data given the probabilities \vec{\theta}.

MLE in multinomial distributions

In a multinomial distribution, the likelihood of observing specific outcomes depends on the probabilities assigned to each category and the observed data.

To estimate \vec{\theta}, we use MLE, which calculates the probabilities as the relative frequencies of each category based on the observed data. This means the estimate for each category’s probability is simply the proportion of observations in that category.

MAP estimate for the Dirichlet distribution

The MAP estimate for the Dirichlet distribution provides the most likely set of probabilities \vec{\theta} given both the observed data and the prior beliefs. It maximizes the posterior distribution.

💡Add-1 (Laplace) Smoothing:
When all \alpha_k = 2, the MAP estimate simplifies to adding 1 to each observed count. This is called Add-1 smoothing, which ensures that no category has zero probability, even if it wasn’t observed in the data. This avoids the zero-count problem and prevents the model from overfitting by making predictions more balanced and allowing for unseen categories.

❓

• Describe the Dirichlet-multinomial model. What are its parameters and its hyperparameters? What do they represent? How is prediction performed if we use a MAP estimate for the parameters? And if we use fully Bayesian inference?
  general concepts of the whole introduction, not necessarily from this page
• What is the difference between classification, regression, and structured prediction?
• What is meant by the “curse of dimensionality”? Why may it impact certain machine learning models?
• What is underfitting? What is overfitting? How can we diagnose these cases? And how can we avoid/mitigate?