The Hough transform is renowned for its ability to detect shapes, patterns, and geometric structures within digital images. Originally devised by Paul Hough in the early 1960s for detecting lines in binary images, the Hough transform has since evolved into a versatile tool capable of identifying various shapes, including lines, circles, ellipses, and more complex curves. By transforming the image space into what we’ll call parameter space, the Hough transform enables the detection of shapes through the accumulation of evidence from edge points or other feature points.
For example, by considering the image on the left, we can firstly apply an edge detection algorithm, then, using the Hough transform, we can get the image on the right, in which all the lines present in the image get highlighted.

Mathematically, the Hough transform considers a line passing through a point (x, \, y) that has equation
y = ax + b
We can rewrite it as
b=-xa+y
Which shows how every point in the (x, \, y) plane—for example the points (x_i, \, y_i) and (x_j, \, y_j)—corresponds to another point in the (a, \, b) plane, which we’ll call the parameter space. Such parameter space is also called ab-plane.
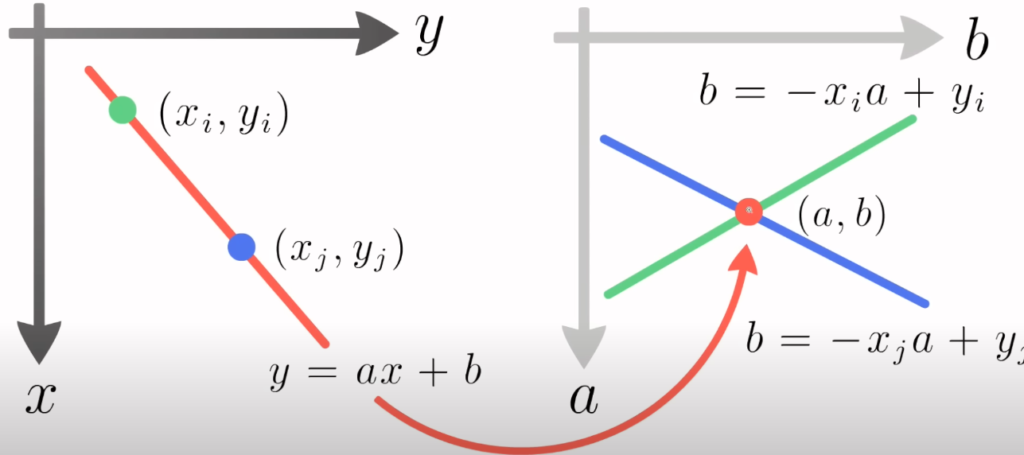
Points that belong to the same line in the (x, \, y) plane will intersect together in their line-representation in the (a, \, b) plane.
We now encounter a problem: a vertical line in the (x, \, y) space cannot be represented in the (a, \, b) space as it would have an angular coefficient that goes to infinity. Therefore we need to find a different way for representing it: the normal representation.
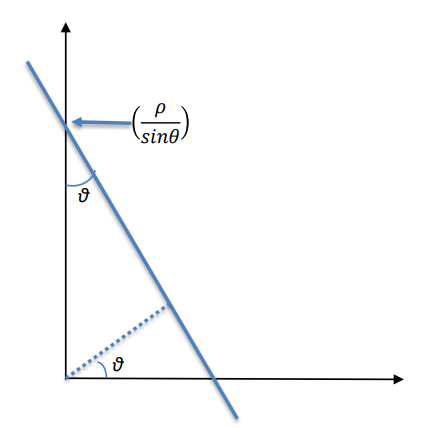
By representing the (x, \, y) plane as
x \cos(\theta) + y \sin(\theta) = \rho
We can isolate y as
\tag{$\spades$}y = -\dfrac{\cos(\theta)}{\sin(\theta)}\cdot\,x+\dfrac{\rho}{\sin(\theta)}This way, (\spades) can be graphically represented as
For example, by running the algorithm on an input image, we get the following representation:

Each of the edges is made up of many different points in the (x, \, y) plane, which, in the feature space, yield to the intersection of multiple lines, that can be represented using a lighter color.
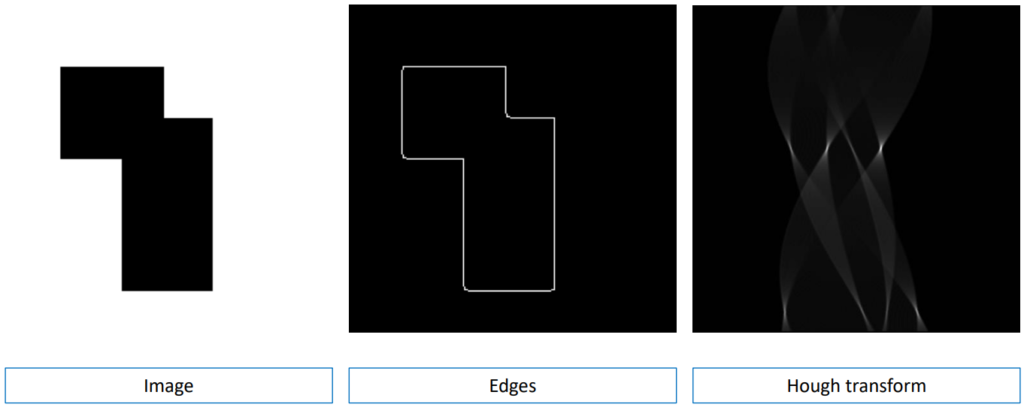
Note: because the image above has 8 edges, the Hough transform based off that image will have 8 points represented in a lighter color. Those regions are called accumulation cells.
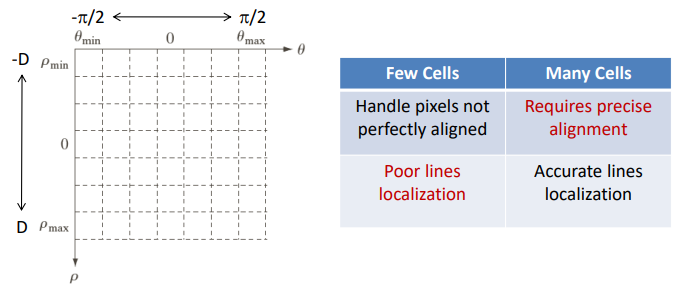
Accumulation cells
By visually inspecting the image example, we can clearly see that there are some accumulation points that appear lighter. The parameter space in normal form is in fact quantized along \rho and \theta. In fact
The curves add up like
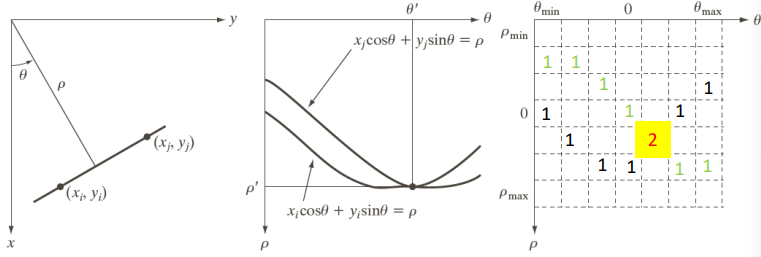
For example:

Generalized Hough transform
The Hough transform works in higher dimensions than two as well. The general equation is in fact
g({\bf v}, \, {\bf c})=0Where {\bf v} is a vector of coordinates and {\bf c} is a vector of coefficients. For example, in the case of a circle, we get
(x-c_1)^2 + (y-c_2)^2=c_3^2
We can therefore use it to find circular shapes